Teleparse

Teleparse is a powerful library designed for creating parsers for custom languages. This book serves as a comprehensive tutorial for using the library and provides a brief introduction to the essential concepts of lexical analysis and syntax analysis, which play crucial roles in compiler design. For more technical details, please refer to the documentation on docs.rs.

Features

• Utilizes Rust's powerful proc-macro system to simplify language declaration, ensuring excellent synergy between data structures and the language being parsed. There's no need to learn a DSL for parser declaration.
• Includes an LL(1) top-down, recursive-descent, non-back-tracking parser. The grammar can be verified as LL(1) through generated tests.
• Offers utilities for parsing common language constructs, such as optional symbols and symbol-delimited lists, with built-in error detection and recovery.
• No separate build tool needed to generate parser code.

Credits

• The "Dragon Book" Compilers: Principles, Techniques, and Tools by Alfred V. Aho, Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman, used as reference for implementation.
• The lexer implementation is backed by the ridiculously fast logos library

Install

Add teleparse as a dependency in your project:

$ cargo add teleparse

It is recommended to import the teleparse::prelude module in your module that interfaces with teleparse to bring all required traits, macros and utility types into scope. You will see almost all the examples do this.

#![allow(unused)]
fn main() {
use teleparse::prelude::*;
}

Textbook Example

In many tutorials that talk about compiler design, the example used is parsing a math expressions consist of variables (identifiers), +, *, and parenthese (( and )). For example, the following are valid expressions:

a + b * c
(a + b) * c
(a + b) * (c + d)

The grammar can be described verbally as follows:

• An expression (E) is a list of terms (T) separated by +.
• A term (T) is a list of factors (F) separated by *.
• A factor (F) is either an identifier or an expression enclosed in parentheses.

You may also seen the following used to describe the above. (It's called Backus-Naur Form or BNF. It's ok if you don't understand this for now. Some places might have ::= instead of =>.)

E  => T E'
E' => + T E' | ε
T  => F T'
T' => * F T' | ε
F  => ( E ) | id

This can almost be translated directly into Rust code with teleparse. Some helper structs are needed to avoid loops when calculating trait requirements, which are annotated with comments.

use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(ignore(r#"\s+"#))]
pub enum TokenType {
    #[teleparse(regex(r#"\w+"#), terminal(Ident))]
    Ident,
    #[teleparse(terminal(OpAdd = "+", OpMul = "*",))]
    Op,
    #[teleparse(terminal(ParenOpen = "(", ParenClose = ")"))]
    Paren,
}

#[derive_syntax]
#[teleparse(root)]
struct E {
    first: T,
    rest: Eprime,
}

// Eplus has to be a separate struct because of recursion when
// computing trait satisfaction. See chapter 3.2 Note on Recursion for more details
#[derive_syntax]
struct Eprime(tp::Option<Eplus>);

#[derive_syntax]
struct Eplus {
    op: OpAdd,
    _t: T,
    rest: Box<Eprime>,
}

#[derive_syntax]
struct T {
    first: F,
    rest: Tprime,
}

#[derive_syntax]
struct Tprime(tp::Option<Tstar>);

#[derive_syntax]
struct Tstar {
    op: OpMul,
    _f: F,
    rest: Box<Tprime>,
}

#[derive_syntax]
enum F {
    Ident(Ident),
    Paren((ParenOpen, Box<E>, ParenClose)),
}

#[test]
fn main() -> Result<(), teleparse::GrammarError> {
    let source = "(a+b)*(c+d)";
    let _ = E::parse(source)?;

    Ok(())
}

Textbook Example - Simplified

Let's revisit the textbook example and the verbal description:

• An expression (E) is a list of terms (T) separated by +.
• A term (T) is a list of factors (F) separated by *.
• A factor (F) is either an identifier or an expression enclosed in parentheses.

E  => T E'
E' => + T E' | ε
T  => F T'
T' => * F T' | ε
F  => ( E ) | id

Notice that the verbal description is much easier to understand than the formal grammar. This is because in the formal grammar, concepts like "list of" and "separated by" need to be broken down to primitives and be defined using helper productions (rules). E' and T' in the example are helpers to define the "list of" concept.

Teleparse, on the other hand, encapsulates these concepts into helper data structures that you can use directly in your language definition. This makes the data structures map closer to the verbal description.

In this example, the tp::Split<T, P> type is used to parse "list of T separated by P with no trailing separator".

use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(ignore(r#"\s+"#))]
pub enum TokenType {
    #[teleparse(regex(r#"\w+"#), terminal(Ident))]
    Ident,
    #[teleparse(terminal(OpAdd = "+", OpMul = "*",))]
    Op,
    #[teleparse(terminal(ParenOpen = "(", ParenClose = ")"))]
    Paren,
}

#[derive_syntax]
#[teleparse(root)]
struct E {
    terms: tp::Split<T, OpAdd>,
}

#[derive_syntax]
struct T {
    factors: tp::Split<F, OpMul>,
}
#[derive_syntax]
enum F {
    Ident(Ident),
    Paren((ParenOpen, Box<E>, ParenClose)),
}

#[test]
fn main() -> Result<(), teleparse::GrammarError> {
    let source = "(a+b)*(c+d)";
    let _ = E::parse(source)?;

    Ok(())
}

Overview of Concepts

Parsing refers to the process of analyzing text (the source code) and creating a data structure that is easier to work with. There are 3 main stages in parsing:

1. Lexical Analysis: Breaks the source code into tokens like keywords, identifiers, literals, etc. For example, the input "struct Foo;" may be broken down to struct, Foo, and ;.
2. Syntax Analysis: Checks the structure of the tokens to see if they form a valid syntax. For example, struct Foo; is valid Rust, but struct; is not.
3. Semantic and other checks: This can involve type checking, name resolution, etc. Teleparse offers some support for this through semantic tokens and hooks, but it's not the main focus.

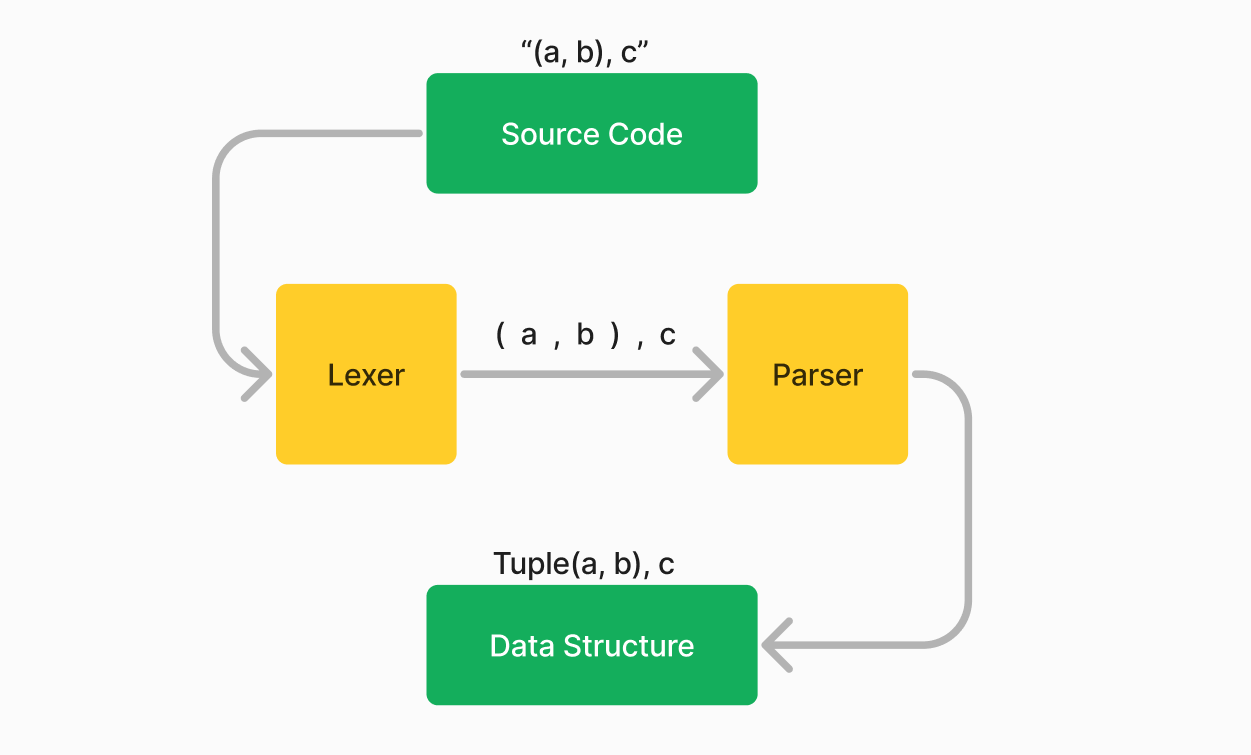
The book will go through how to use teleparse for each stage.

Lexical Analysis

The #[derive_lexicon] macro is used to declare token types and lexical analyzer rules (the lexer rules) using an enum. It was already showcased in the beginning of the book with the full example. Let's take a closer look here.

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(ignore(r"\s"))] // ignore whitespaces
pub enum TokenType {

    /// Numbers in the expression
    #[teleparse(regex(r"\d+"), terminal(Integer))]
    Integer,

    /// The 4 basic operators
    #[teleparse(terminal(
        OpAdd = "+", 
        OpMul = "*", 
    ))]
    Operator,

    /// Parentheses
    #[teleparse(terminal(ParenOpen = "(", ParenClose = ")"))]
    Paren,
}
}

Attributes on the enum:

• #[derive_lexicon] is the entry point, and processes the other teleparse attributes.
• #[teleparse(ignore(...))] defines the patterns that the lexer should skip between tokens.
  • You can speify multiple regexes like #[teleparse(ignore(r"\s+", r"\n+"))].

Attributes on the variants:

• #[teleparse(terminal(...))] generates structs that can be used to put in the syntax tree.
  • The example generates Integer, OpAdd, OpMul, ParenOpen and ParenClose structs.
  • Some have a specific literal value to match. For example, OpAdd will only match a token of type Op that is the + character.
• #[teleparse(regex(...))] defines the pattern to match for the token type.

Understanding Terminals

Terminals are leaf nodes in the syntax tree. For example, in the "textbook" grammar:

E  => T E'
E' => + T E' | ε
T  => F T'
T' => * F T' | ε
F  => ( E ) | id

The syntax ... => ... is called a production. The left-hand side is the symbol to produce, and the right-hand side is what can produce it. The left-hand symbol is also called a non-terminal, and every symbol on the right-hand side that does not appear on the left-hand side is a terminal.

In this example, +, *, (, ), and id are terminals. The other symbols are non-terminals.

The terminal structs derived by #[derive_lexicon] are the building blocks to define the syntax tree. For example:

use teleparse::prelude::*;
use teleparse::GrammarError;

#[derive_lexicon]
#[teleparse(ignore(r"\s+"), terminal_parse)]
pub enum TokenType {
    #[teleparse(regex(r"\w+"), terminal(Id))]
    Ident,
}

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq)] // for assert_eq!
struct ThreeIdents(Id, Id, Id);

#[test]
fn main() -> Result<(), GrammarError> {
    let t = ThreeIdents::parse("a b c")?;
    assert_eq!(
        t,
        Some(ThreeIdents(
            Id::from_span(0..1),
            Id::from_span(2..3),
            Id::from_span(4..5),
        ))
    );

    let pizza = Id::parse("pizza")?;
    assert_eq!(pizza, Some(Id::from_span(0..5)));

    Ok(())
}

Here:

• We are generating a Id terminal to parse a token of type Ident, matching the regex r"\w+".
• We are creating a non-terminal ThreeIdents with the production ThreeIdents => Id Id Id.
  • More about #[derive_syntax] in later sections
• We are also using the terminal_parse attribute to derive a parse method for the terminals for testing purposes.

Using regex and terminal attributes

The #[teleparse(regex(...))] and #[teleparse(terminal(...))] attributes are used to define the pattern to match for the token type and terminals in the syntax tree.

The simpliest example is to define a single terminal struct, along with a regex for the lexer to produce the token type when the remaining source code matches the regex.

use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(terminal_parse)]
pub enum MyToken {
    #[teleparse(regex(r"\w+"), terminal(Ident))]
    Ident,
}

fn main() {
    assert_eq!(Ident::parse("hell0"), Ok(Some(Ident::from_span(0..5))));
}

You can also add additional terminals that have to match a specific literal value.

use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(terminal_parse)]
pub enum MyToken {
    #[teleparse(regex(r"\w+"), terminal(Ident, KwClass = "class"))]
    Word,
}

fn main() {
    let source = "class";
    // can be parsed as Ident and KwClass
    assert_eq!(Ident::parse(source), Ok(Some(Ident::from_span(0..5))));
    assert_eq!(KwClass::parse(source), Ok(Some(KwClass::from_span(0..5))));
    // other words can only be parsed as Ident
    let source = "javascript";
    assert_eq!(Ident::parse(source), Ok(Some(Ident::from_span(0..10))));
    assert_eq!(KwClass::parse(source), Ok(None));
}

When such literals are present specified for the terminals along with the regex for the variant, derive_lexicon will do some checks at compile-time to make sure the literals make sense.

For each literal, the regex must:

• has a match in the literal that starts at the beginning (position 0)
• the match must not be a proper prefix of the literal

For the first condition, suppose the regex is board and the literal is keyboard. The lexer will never be able to emit keyboard when the rest of the input starts with board.

use teleparse::prelude::*;

#[derive_lexicon]
pub enum MyToken {
    #[teleparse(regex("board"), terminal(Board, Keyboard = "keyboard"))]
    DoesNotMatchTerminal, 
}

fn main() {}

error: This regex does not match the beginning of `keyboard`. This is likely a mistake, because the terminal will never be matched
 --> tests/ui/lex_regex_not_match_start.rs:5:23
  |
5 |     #[teleparse(regex("board"), terminal(Board, Keyboard = "keyboard"))]
  |                       ^^^^^^^

For the second condition, suppose the regex is key and the literal is keyboard. The lexer will again never be able to emit keyboard:

• If it were to emit keyboard of this token type, the rest of the input must start with keyboard
• However, if so, the lexer would emit key instead

use teleparse::prelude::*;
#[derive_lexicon]
pub enum MyToken {
    #[teleparse(regex("key"), terminal(Key, Keyboard = "keyboard"))]
    DoesNotMatchTerminal, 
}

fn main() {}

error: This regex matches a proper prefix of `keyboard`. This is likely a mistake, because the terminal will never be matched (the prefix will instead)
 --> tests/ui/lex_regex_not_match_is_prefix.rs:4:23
  |
4 |     #[teleparse(regex("key"), terminal(Key, Keyboard = "keyboard"))]
  |                       ^^^^^

Inferring the regex pattern from terminals

If a token type should only produce terminals with known literal values (for example, a set of keywords), regex can be omitted since it can be inferred from the terminals.

use teleparse::prelude::*;

#[derive_lexicon]
#[teleparse(terminal_parse)]
pub enum MyToken {
    #[teleparse(terminal(Pizza = "pizza", Pasta = "pasta"))]
    Food,
}

fn main() {}

This is the Don't-Repeat-Yourself (DRY) principle. In fact, derive_lexicon enforces it:

use teleparse::prelude::*;

#[derive_lexicon]
pub enum TokenType {
    #[teleparse(terminal(
        OpAdd = "+", 
        OpSub = "-", 
        OpMul = "*", 
        OpDiv = "/",
    ), regex(r"[\+\-\*/]"))]
    Operator,
}

fn main() {}

error: Defining `regex` here is redundant because all terminals have a literal match pattern, so the rule can already be inferred.
  --> tests/ui/lex_redundant_regex.rs:11:5
   |
11 |     Operator,
   |     ^^^^^^^^

Handling Comments (Extracted Tokens)

Comments are special tokens that don't have meaning in the syntax and are there just for human readers.

You may recall that you can skip unwanted patterns between tokens by using #[teleparse(ignore(...))]. This can be used for comments, but sometimes you do want to parse the comments. For example for a transpiler that keeps the comments in the output.

In this senario, you can define a token type that doesn't have any terminals. The lexer will still produce those tokens, but instead of passing them to the parser, they will be kept aside. You can query them using a Parser object later.

use teleparse::prelude::*;

#[derive_lexicon]
pub enum MyToken {
    #[teleparse(regex(r"/\*([^\*]|(\*[^/]))*\*/"))]
    Comment,
}

fn main() {
    let input = "/* This is a comment */";
    // you can call `lexer` to use a standalone lexer without a Parser
    let mut lexer = MyToken::lexer(input).unwrap();
    // the lexer will not ignore comments
    assert_eq!(
        lexer.next(),
        (None, Some(Token::new(0..23, MyToken::Comment)))
    );
    // `should_extract` will tell the lexer to not return the token to the Parser
    assert!(MyToken::Comment.should_extract());
}

Lexer Validation

There are additional restrictions that are enforced at compile-time apart from the ones covered previously

Duplicated Terminals

Having duplicated terminals is likely a mistake, because those terminals are interchangeable in the syntax tree. Likewise, you cannot have 2 terminals with no literals.

use teleparse::prelude::*;
#[derive_lexicon]
pub enum MyToken {
    #[teleparse(terminal(Zero = "0", Another = "0"))]
    Integer,
}
fn main() {}

error: Duplicate literal pattern `0` for variant `Integer`.
 --> tests/ui/lex_no_dupe_literal.rs:4:48
  |
4 |     #[teleparse(terminal(Zero = "0", Another = "0"))]
  |                                                ^^^

Regex Features

Teleparse uses the logos crate for the lexer, which combines all the rules into a single state machine for performance. Logos also imposes additional restrictions on regex features that requires backtracking. Please refer to their documentation for more information.

Syntax Analysis

The #[derive_syntax] macro turns a struct or enum into a syntax tree node as part of the Abstract Syntax Tree , or AST. These become the non-terminal symbols of your language.

Structs

Structs are used to define sequences of symbols. For example, this production:

X => A B C

Means to produce X, you need to produce A, B, and C in that order.

For a more real-world example, say we want to parse an assignment statement like x = 1. For simplicity, we will assume the right hand side is always a number.

AssignmentStatement => Ident OpAssign Number

Suppose Ident, OpAssign and Number are all terminals created with #[derive_lexicon], we can create AssignmentStatement like this:

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
pub struct AssignmentStatement(pub Ident, pub OpAssign, pub Number);
}

Named fields work as well:

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
pub struct AssignmentStatement {
    pub ident: Ident,
    pub op_assign: OpAssign,
    pub number: Number,
}
}

When the parser is expecting an AssignmentStatement, it will try to parse Ident, then OpAssign, then Number, and put them in the struct.

Enums

Enums are used to define choices (unions) of productions. Continuing our example with AssignmentStatement, suppose we want to create a Statement that can either be an assignment or a function call.

This can be denoted with

Statement => AssignmentStatement | FunctionCallStatement

We can create Statement like this:

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
pub enum Statement {
    Assignment(AssignmentStatement),
    FunctionCall(FunctionCallStatement),
}
}

When the parser is expecting a Statement, it will try to parse either an AssignmentStatement or a FunctionCallStatement, and create a Statement with the corresponding variant. We will cover how the parser decides which path to take in the next section.

Root

With the terminals and non-terminals, we can build the data structures for the entire language. On the outermost level, there will be one symbol that is the "target" to parse. We will refer to it as the root. For example, for a programming language, the root might be the syntax for a file.

To indicate the symbol is root, use the #[teleparse(root)] attribute.

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
#[teleparse(root)]
pub struct File {
    ...
}
}

This will derive the Root trait, which has a parse() function that can be called to parse an input string to the root symbol. For more complex usage, you can use the Parser object.

LL(1)

Teleparse forces the grammar created with #[derive_syntax] to be LL(1), which stands for:

• The parser scans the input Left to right
• The parser derives the Leftmost tree first
• The parser only ever looks 1 token ahead

These rules help the parser to be more efficient. The parser will only need to look at the next token to decide what to parse next, and it does not require backtracking.

To validate the grammar is LL(1), the #[teleparse(root)] attribute generates a test that can be ran with cargo test that fails if the grammar is not LL(1). For example, the following grammar is not LL(1):

Decl      => PubEnum | PubStruct
PubEnum   => pub enum
PubStruct => pub struct

When parsing Decl, if the next token is pub, the parser will not know whether to parse PubEnum or PubStruct, since both start with pub. If we implement this grammar with Teleparse, the generated test will fail with a message to help you debug the issue.

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_lexicon]
pub enum TokenType {
    #[teleparse(terminal(KwPub = "pub", KwEnum = "enum", KwStruct = "struct"))]
    Keyword,
}

#[derive_syntax]
pub struct PubEnum {
    pub kw_pub: KwPub,
    pub kw_enum: KwEnum,
}

#[derive_syntax]
pub struct PubStruct {
    pub kw_pub: KwPub,
    pub kw_struct: KwStruct,
}

#[derive_syntax]
#[teleparse(root)]
pub enum Decl {
    PubEnum(PubEnum),
    PubStruct(PubStruct),
}
}

thread 'Decl_root_test::is_ll1' panicked at <source location>
Decl is not LL(1): The non-terminal `Decl` has a FIRST/FIRST conflict producing either `PubEnum` or `PubStruct`. The conflict
ing terminals are: "pub"
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

We can rewrite the grammar to resolve the conflict:

Decl         => pub EnumOrStruct
EnumOrStruct => enum | struct

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_lexicon]
pub enum TokenType {
    #[teleparse(terminal(KwPub = "pub", KwEnum = "enum", KwStruct = "struct"))]
    Keyword,
}

#[derive_syntax]
pub enum EnumOrStruct {
    Enum(KwEnum),
    Struct(KwStruct),
}

#[derive_syntax]
#[teleparse(root)]
pub struct Decl {
    pub kw_pub: KwPub,
    pub data: EnumOrStruct,
}
}

Note that there are other conditions that make a grammar not LL(1). If you are unsure how to resolve them, please utilize search engines to learn more about LL(1) grammars and how to resolve conflicts.

Note on Recursion

Consider again the example shown in the beginning of the book:

E  => T E'
E' => + T E' | ε
T  => F T'
T' => * F T' | ε
F  => ( E ) | id

Note that this grammar involves recursions. For example, the productions of E' and T' involve themselves; and production of E involves F indirectly, which in turn involves E.

There are 2 things to note when implement a grammar that has recursion:

1. The data structure must have a finite size. This can be easily achieved by using a Box.
2. There must NOT be recursion when computing if trait requirements are satisfied.

We will go through an example to illustrate both points. Suppose we are implementing E' as:

#![allow(unused)]
fn main() {
// E' => + T E' | ε
#[derive_syntax]
struct Eprime(tp::Option<(OpAdd, T, Eprime)>);
}

Note we are using tp::Option to represent the ε case. This is a utility type used to represent optional values. Utility types will be covered in the next chapter.

The first error you will get is:

recursive type `Eprime` has infinite size

This is because Eprime contains Eprime itself, creating an infinite recursion when calculating the size. To fix this, we can box the recursive part:

#![allow(unused)]
fn main() {
#[derive_syntax]
struct Eprime(tp::Option<(OpAdd, T, Box<Eprime>)>);
}

Now we will see the second error:

Overflow evaluating the requirement `Eprime: Produce`

This error message is a little cryptic. One might think it's related to having Eprime referenced in itself. However, the root cause is that derive_syntax infers the lexicon type by looking at the first fields of structs and first variants of enums. We can walk through how Rust is evaluating this:

1. The lexicon type of Eprime is the same as the lexicon type of tp::Option<(OpAdd, T, Box<Eprime>)>.
2. The lexicon type of tp::Option<(OpAdd, T, Box<Eprime>)> is the same as that of (OpAdd, T, Box<Eprime>).
3. The lexicon type of (OpAdd, T, Box<Eprime>) is the same as that of OpAdd, T, and Box<Eprime>, and they must be the same (according to the trait implementation for tuples)
4. The lexicon type of OpAdd is TokenType.
5. The lexicon type of T is TokenType, which is the same as that of OpAdd.
6. The lexicon type of Box<Eprime> is the same as that of Eprime.
7. We are already calculating the lexicon type of Eprime, resulting in overflow

To fix this, the example in the beginning of the book uses a separate struct Eplus to avoid the loop:

#![allow(unused)]
fn main() {
#[derive_syntax]
struct Eprime(tp::Option<Eplus>);

#[derive_syntax]
struct Eplus {
    op: OpAdd,
    _t: T,
    rest: Box<Eprime>,
}
}

In this case, the lexicon type of Eplus does not depend on Eprime, because derive_syntax generates an implementation for Eplus instead of relying on blanket trait implementation as in the tuple case.

Another place where this error can appear is in enums. In the following example, Paren must not be the first variant of the enum.

#![allow(unused)]
fn main() {
#[derive_syntax]
enum F {
    Ident(Ident),
    Paren((ParenOpen, Box<E>, ParenClose)),
}
}

Remove Recursion with Utility Types

In the first example above, the grammar requires recursion in E' to implement a list-like structure (terms separated by +). Teleparse provides utility types like tp::Split to simplify the implementation and provide out-of-the-box support for panic recovery. Utility types are covered in Chapter 4.

Utility Types

The teleparse::tp module provides utility types for language constructs that are hard to or not directly representable in a grammar. For example, a list of items separated by a delimiter,

Examples of Common Utility Types

There are other utility types that are used less often.

Blanket Types

Besides the utility types above, teleparse also provide syntax tree implementation for some types in the Rust standard library:

• Box<T> for any syntax tree T
• Tuples up to 5 elements (e.g. (T1, T2, T3, T4, T5))

Option

tp::Option<T> and tp::Exists<T> are types used to represent optional syntax trees. tp::Option<T> stores the syntax tree itself, and tp::Exists<T> stores a boolean value to test if the syntax tree is present.

Production

Option<T> => ε | T

Example

Ident is a terminal struct not shown here

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq)]
struct OptIdent(tp::Option<Ident>);

#[test]
fn test_none() -> Result<(), GrammarError> {
    let t = OptIdent::parse("+")?.unwrap();
    assert_eq!(t, OptIdent(Node::new(0..0, None).into()));

    Ok(())
}

#[test]
fn test_some() -> Result<(), GrammarError> {
    let t = OptIdent::parse("a")?.unwrap();
    assert_eq!(t, OptIdent(Node::new(0..1, Some(Ident::from_span(0..1)).into()));

    Ok(())
}
}

Deref

tp::Option<T> / tp::Exists<T> implements Deref and DerefMut. So you can use them as &std::option::Option<T> / &bool.

#![allow(unused)]
fn main() {
let t = OptIdent::parse("a")?.unwrap();
assert!(t.0.is_some());
}

Parsing

There are 3 possible outcomes when parsing an Option<T>:

1. The next token is not in FIRST(T). The parser will return None.
2. The next token is in FIRST(T):
   1. If the parser can parse T, it will return Some(T).
   2. If the parser cannot parse T, it will record an error, return None, and continue.

In any case, the parser will not panic.

Common LL(1) Violations

1. Option<Option<T>> - since Some(None) and None are indistinguishable.
2. (Option<T>, T) - since (None, T) and (Some(T), ...) are indistinguishable.

String

These types are used to access the source of the syntax tree. For example, getting the name of a variable.

• tp::Parse<S: FromStr, T> is used for types that implement FromStr, such as numeric types. It stores the parse result.
• tp::Quote<S: From<&str>, T> on the other hand, stores the string value directly.
• tp::String is an alias for tp::Quote<String, T>.

Example

Ident and Integer are terminal structs not shown here.

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq, Clone)]
struct Parsed {
    ident: tp::Parse<u32, Ident>,
    num: tp::Parse<u32, Integer>,
    float: tp::Parse<f32, Integer>,
}

#[test]
fn test_parse() {
    let t = Parsed::parse("abc 456 314").unwrap().unwrap();
    assert!(t.ident.is_err());
    assert_eq!(t.num, Node::new(4..7, Ok(456)).into());
    assert_eq!(t.float, Node::new(8..11, Ok(314.0)).into());

    assert_eq!(*t.num, Ok(456));
    assert_eq!(*t.float, Ok(314.0));
}
}

Deref

tp::Parse can be dereferenced to the parse Result, and tp::Quote can be dereferenced to the inner string value.

#![allow(unused)]
fn main() {
#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq, Clone)]
struct Stringified(tp::String<Ident>);

let t = Stringified::parse("a").unwrap().unwrap();
assert_eq!(&*t.0, "a");
}

Parsing

The string types parse exactly the same as the inner syntax tree type T. After parsing is successful, the content is parsed/copied to the corresponding type.

If you want to avoid copying, you can use the inner type directly (which usually only stores a span), and use the span to access the source string when needed.

Iteration

These types are used to parse a list of items directly after one another (i.e. without a delimiter), and stops if the item cannot start with the next token.

• tp::Plus<V: FromIterator<T>, T> is one or more of T
• tp::Star<V: FromIterator<T> + Default, T> is zero or more of T
• tp::Vec<T> and tp::VecDeque<T> are aliases for tp::Star<Vec<T>, T> and tp::Star<VecDeque<T>, T> respectively
• tp::Nev<T> and tp::NevDeque<T> are aliases for tp::Plus<Vec<T>, T> and tp::Plus<VecDeque<T>, T> respectively. Nev stands for "non-empty vector".

The name "Plus" and "Star" are borrowed from regular expression notation "+" and "*" to indicate "one or more" and "zero or more" respectively.

Production

Plus<T> => T Star<T>
Star<T> => Option<Plus<T>>

Examples

Ident is a terminal struct not shown here

#![allow(unused)]
fn main() {
use teleparse::prelude::*;
use teleparse::GrammarError;

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq, Clone)]
struct IdentList(tp::Nev<Ident>);

#[test]
fn parse() -> Result<(), GrammarError> {
    let t = IdentList::parse("a b c  d e").unwrap();
    assert_eq!(
        t,
        IdentList(
            Node::new(
                0..10,
                vec![
                    Ident::from_span(0..1),
                    Ident::from_span(2..3),
                    Ident::from_span(4..5),
                    Ident::from_span(7..8),
                    Ident::from_span(9..10),
                ]
            )
            .into()
        )
    );

    Ok(())
}
}

Deref

Plus and Star can be dereferenced to the inner vector type. For example, you can use tp::Vec<T> as a &std::vec::Vec<T>.

Parsing

Plus and Star share similar parsing logic. The only difference is that if the next token is not in FIRST(T), the parser will return Default::default() for Star but will panic for Plus.

The parser keeps trying to parse T while the next token is in FIRST(T). If the parser panics while parsing T, it will record the error and recover with the items already parsed. The only exception is the first item in a Plus, in which case the parser panics instead.

Common LL(1) Violations

1. Vec<Option<T>> - since there can be an infinite number of Nones.

Delimited List

These types are used to parse a list of items separated by a delimiter. Error recovery is possible for these types with the help of the delimiter. See Error Recovery below.

• tp::Split<T, P> is used to parse a list of T separated by a delimiter P.
• tp::Punct<T, P> is used to parse a list of T separated by a delimiter P, with optional trailing delimiter.

Neither list types are allowed to be empty. If you need to parse an empty list, wrap it with tp::Option.

Production

Split<T, P> => T Star<(P, T)>
Punct<T, P> => T Option<(P, Option<Punct<T, P>)>

Examples

Ident and OpAdd are terminal structs not shown here

#![allow(unused)]
fn main() {
use teleparse::prelude::*;
use teleparse::GrammarError;

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq)]
struct Terms(tp::Split<Ident, OpAdd>);

#[test]
fn parse_one() -> Result<(), GrammarError> {
    let mut parser = Parser::new("a + b + c")?;
    let terms = parser.parse::<Terms>()?.unwrap();

    let mut iter = terms.iter();
    assert_eq!(iter.next(), Some(Ident::from_span(0..1)));
    assert_eq!(iter.next(), Some(Ident::from_span(4..5)));
    assert_eq!(iter.next(), Some(Ident::from_span(8..9)));
    assert_eq!(iter.next(), None);

    Ok(())
}
}

Deref

Split<T, P> and Punct<T, P> can be dereferenced as a vector of the items T (&Vec<T>). The delimiters can be accessed using the puncts field.

Error Recovery

When the parser fails to parse an item T:

• Split will record an error, and stop if the next token is in FOLLOW(Split<T>)
• Punct will only record an error if the next token is not in FIRST(T) or FOLLOW(Punct<T>), because it's possible to end on a delimiter.

Otherwise, it will try to recover:

• If the next token is in FIRST(P), it will skip this item and continue with parsing the delimiter.
• Otherwise, it will skip tokens until a token in FIRST(P), FIRST(T) or FOLLOW(self) is found.

Also note that there can be multiple delimiters between 2 elements because of recovery. You cannot assume any relationship between the number and positions of the delimiters and the elements.

Recover

The tp::Recover<T, R> type adds recover logic. It's equivalent production-wise to (T, R), but if T or R fails to parse, the parser will skip tokens until an R can be parsed.

The head and tail fields are used to access T and R respectively.

Production

Recover<T, R> => T R

Example

Ident and Semi are terminal structs not shown here

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_syntax]
#[teleparse(root)]
#[derive(Debug, PartialEq)]
struct Statement(tp::Recover<Ident, Semi>);

#[test]
fn parse_ok() -> Result<(), GrammarError> {
    let t = Statement::parse("a;")?;
    assert_eq!(
        t,
        Some(Statement(tp::Recover {
            head: Node::new(0..1, Some(Ident::from_span(0..1))),
            tail: Semi::from_span(1..2),
        }))
    );

    Ok(())
}

#[test]
fn parse_recover() -> Result<(), GrammarError> {
    let t = Statement::parse("1;")?;
    assert_eq!(
        t,
        Some(Statement(tp::Recover {
            head: Node::new(0..1, None),
            tail: Semi::from_span(1..2),
        }))
    );

    Ok(())
}
}

Loop

The tp::Loop<T> type is also a list of T (like Plus and Star), but it will keep skipping tokens when parsing T fails until the end of input.

This is useful if the root should be a list of items, and you may want to skip invalid tokens in between.

Production

Loop<T> => T Loop<T>

Deref

Just like Plus and Star, Loop<T> can be dereferenced to &Vec<T>.

Semantic

The same token type can have different semantic meaning in different contexts. For example, the Rust code below:

fn main() {
    let x = 1;
}

main and x are both identifiers, but main is a function name and x is a variable name. One use case for this is syntax highlighting where different colors can be displayed for the two words, for example.

To add a semantic type, add an variant to the enum with derive_lexicon without any teleparse attribute:

#![allow(unused)]
fn main() {
use teleparse::prelude::*;

#[derive_lexicon]
pub enum TokenType {
    #[teleparse(regex(r#"[a-zA-Z]+"#), terminal(Ident))]
    Ident,
    #[teleparse(terminal(OpEq = "="))]
    Op,
    VariableName, // <- semantic type
}
}

Then add a #[teleparse(semantic(...))] attribute in the syntax tree. Multiple semantic types can be added by separating them with ,

#![allow(unused)]
fn main() {
#[derive_syntax]
pub struct Assignment {
    #[teleparse(semantic(VariableName))]
    pub variable: Ident,
    pub op: OpEq,
    pub expression: Ident,
}
}

The VariableName semantic type will now be applied to variable.

The semantic info is stored in Parser. You can access it after parsing by using info().tokens

#![allow(unused)]
fn main() {
use teleparse::prelude::*;
use teleparse::{Parser, GrammarError};
fn test() -> Result<(), GrammarError> {
    let source = "a = b";
    let mut parser = Parser::<TokenType>::new(source);
    let assignment = parser.parse::<Assignment>()?.unwrap();

    // Get the token info at `variable`
    let token = parser.info().tokens.at_span(assignment.variable.span()).unwrap();
    assert!(token.semantic.contains(TokenType::VariableName));

    Ok(())
}
}